Merge Sort
Merge sort is a pretty neat algorithm. It relies upon some exceptionally interesting recursive functions that are at least good to see even if you will almost certainly never need to write functions like this in Elm. So read this like a tour of various tricks that expand your expectations, not as exercises that you should find obvious or easy!
Merge sort relies on a couple observations:
- A list with one element is sorted.
- If you keep splitting a list in half, eventually you will have a bunch of lists with one element.
- If you have two sorted lists, merging them into a single sorted list is easy.
That last claim seems kind of dubious. Is it actually easy to merge two sorted lists? Let’s start there.
Merge
First, check out this animation of how we want to merge two sorted lists:
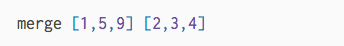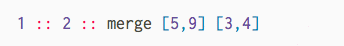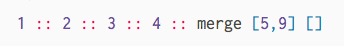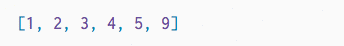
In both lists, the smallest element is the first element. We look at both of those and pick the smallest overall. That becomes the smallest element in our resulting list. We can then repeat this process until we ended up with a merged list. But how do we write the code to do this?!
On the previous page of this book, we said that one strategy for writing recursive functions is to (1) use case and (2) pretend you are done. Let’s try that route:
merge : List comparable -> List comparable -> List comparable
merge listOne listTwo =
case (listOne, listTwo) of
([], []) ->
...
(front :: rest, []) ->
...
([], front :: rest) ->
...
(frontOne :: restOne, frontTwo :: restTwo) ->
...
The first case is the easiest. If both lists are empty, merging them will result in an empty list. The second and third cases are pretty similar. If one lists is empty, merging will result in the other list.
merge : List comparable -> List comparable -> List comparable
merge listOne listTwo =
case (listOne, listTwo) of
([], []) ->
[]
(_ :: _, []) ->
listOne
([], _ :: _) ->
listTwo
(frontOne :: restOne, frontTwo :: restTwo) ->
...
At this point, the three patterns we have implemented kind of overlap in how they work. We can shuffle them around to look like this:
merge : List comparable -> List comparable -> List comparable
merge listOne listTwo =
case (listOne, listTwo) of
(_, []) ->
listOne
([], _) ->
listTwo
(frontOne :: restOne, frontTwo :: restTwo) ->
...
If a list is empty, return the other one. If they are both empty, it will match the first pattern and return listOne which is an empty list! This trick is definitely not necessary, but I hope it is valuable to see.
We are losing focus here. What about that last branch? Well, we know listOne and listTwo are sorted, so it must be true that either frontOne or frontTwo is the lowest value overall. We can check for that:
merge : List comparable -> List comparable -> List comparable
merge listOne listTwo =
case (listOne, listTwo) of
(_, []) ->
listOne
([], _) ->
listTwo
(frontOne :: restOne, frontTwo :: restTwo) ->
if frontOne < frontTwo then
frontOne :: ...
else
frontTwo :: ...
Now it is time for step two of writing a recursive function. Pretend you are done. Wouldn’t it be great if we had a function that could merge all the remaining values? Let’s pretend!
merge : List comparable -> List comparable -> List comparable
merge listOne listTwo =
case (listOne, listTwo) of
(_, []) ->
listOne
([], _) ->
listTwo
(frontOne :: restOne, frontTwo :: restTwo) ->
if frontOne < frontTwo then
frontOne :: merge restOne listTwo
else
frontTwo :: merge listOne restTwo
We take the lowest value off of one of the lists, and then call merge on the leftovers. Now that we have a merge function that can combine two sorted lists, but how do we get those two lists?
Split
We need some split function that can take a list and split it in half into two lists.
split : List a -> ( List a, List a )
split list =
...
Now our trusty two step process says to start with a case expression:
split : List a -> ( List a, List a )
split list =
case list of
[] ->
...
front :: rest ->
...
If we have an empty list, when we split it into two, we will get two empty lists.
split : List a -> ( List a, List a )
split list =
case list of
[] ->
( [], [] )
front :: rest ->
...
At this point it is kind of unclear how to proceed. We need to put front somewhere, but which list should we put it on? I do not really know. Time to try out our second strategy for writing recursive functions: create a helper function that keeps track of extra information. In this case, it would be nice to build up the two half lists as we go along.
split : List a -> ( List a, List a )
split list =
splitHelp list [] []
splitHelp : List a -> List a -> List a -> ( List a, List a )
splitHelp list halfOne halfTwo =
case list of
[] ->
(halfOne, halfTwo)
first :: rest ->
...
In the second case, we have the first value of list, but should we put it on halfOne or halfTwo? We cannot put front on halfOne every time or in the end halfTwo will still be empty! It feels like we need more information... Well, with the helper function strategy, whenever we feel like we need more info, we can just add it as an argument. So let’s start keeping track of a Bool that determines which list we should be adding to:
split : List a -> ( List a, List a )
split list =
splitHelp list True [] []
splitHelp : List a -> Bool -> List a -> List a -> ( List a, List a )
splitHelp list shouldAddToOne halfOne halfTwo =
case list of
[] ->
(halfOne, halfTwo)
first :: rest ->
if shouldAddToOne then
splitHelp rest (not shouldAddToOne) (first :: halfOne) halfTwo
else
splitHelp rest (not shouldAddToOne) halfOne (first :: halfTwo)
Now as we go through the shouldAddToOne value keeps switching between True and False so we end up splitting every other element into separate lists.
Note: There are tons of other ways to implement
splitthat can be fun and educational to explore. For example, having anIntthat increments as you go through and adding to one list or the other depending on whether it is odd or even. There are two implementations that are particularly interesting though, and I wrote about them here. These implementations do not really teach you practical skills, but they are definitely worth checking out!
Sort
Now that we have split and merge, it is time to finally write our sort function. We start like normal, by using case to break things up.
sort : List comparable -> List comparable
sort list =
case list of
[] ->
[]
first :: rest ->
...
To take the next step, let’s take another look at the crucial observations that make merge sort work:
- A list with one element is sorted.
- If you keep splitting a list in half, eventually you will have a bunch of lists with one element.
- If you have two sorted lists, merging them into a single sorted list is easy.
Okay, so a list with zero elements is sorted. A list with one element is sorted. Let’s fill in those facts.
sort : List comparable -> List comparable
sort list =
case list of
[] ->
list
[_] ->
list
_ ->
...
In the last case, we know we have two or more elements. Let’s just start using the functions we have available and see what happens:
sort : List comparable -> List comparable
sort list =
case list of
[] ->
list
[_] ->
list
_ ->
let
(halfOne, halfTwo) =
split list
in
...
Okay, we can split the list in half. Now is the crucial step. Pretend you are done. We know that merging two sorted lists results in a sorted list, so wouldn’t it be wonderful if there was some way to sort halfOne and halfTwo?
sort : List comparable -> List comparable
sort list =
case list of
[] ->
list
[_] ->
list
_ ->
let
(halfOne, halfTwo) =
split list
in
merge (sort halfOne) (sort halfTwo)
I personally found it kind of hard to believe that this works when I first learned it, so I recommend playing with the code here and trying it out on different lists.
Now again, this outline of merge sort is primarily intended to expose you to some exceptionally interesting recursive functions. This is in no way representative of how difficult it is to write functional programs. These are the gems mined by academics over decades, and I just think it is worth taking a look!